PHOTON INTERACTION RATES CONTENTS
Attenuation
As a photon makes its way through matter, there is no way to predict precisely either how far it will travel before engaging in an interaction or the type of interaction it will engage in. In clinical applications we are generally not concerned with the fate of an individual photon but rather with the collective interaction of the large number of photons. In most instances we are interested in the overall rate at which photons interact as they make their way through a specific material.
Let us observe what happens when a group of photons encounters a slice of material that is 1 unit thick, as illustrated in the figure below. Some of the photons interact with the material, and some pass on through. The interactions, either photoelectric or Compton, remove some of the photons from the beam in a process known as attenuation. Under specific conditions, a certain percentage of the photons will interact, or be attenuated, in a 1-unit thickness of material.
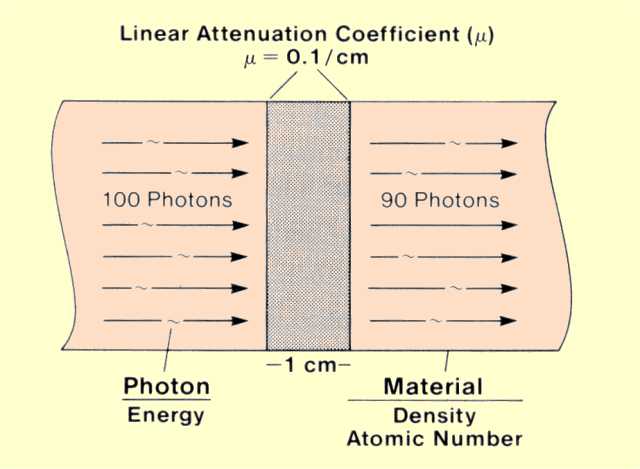
Linear Attenuation Coefficient
The linear attenuation coefficient (µ) is the actual fraction of photons interacting per 1-unit thickness of material. In our example the fraction that interacts in the 1-cm thickness is 0.1, or 10%, and the value of the linear attenuation coefficient is 0.1 per cm.
Linear attenuation coefficient values indicate the rate at which photons interact as they move through material and are inversely related to the average distance photons travel before interacting. The rate at which photons interact (attenuation coefficient value) is determined by the energy of the individual photons and the atomic number and density of the material.
Mass Attenuation Coefficient
In some situations it is more desirable to express the attenuation rate in terms of the mass of the material encountered by the photons rather than in terms of distance. The quantity that affects attenuation rate is not the total mass of an object but rather the area mass. Area mass is the amount of material behind a 1-unit surface area, as shown below. The area mass is the product of material thickness and density:
Area Mass (g/cm2) = Thickness (cm) x Density (g/cm3).
The mass attenuation coefficient is the rate of photon interactions per 1-unit (g/cm2) area mass.
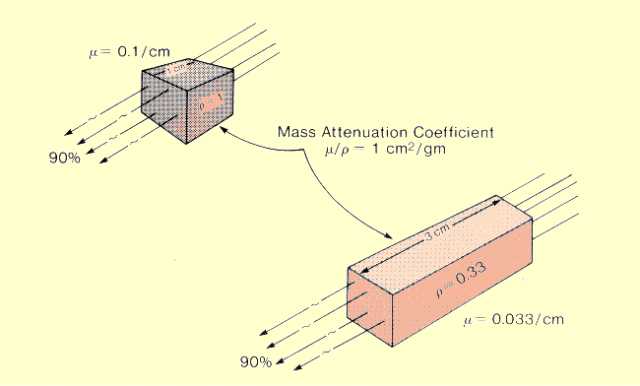
Mass Attenuation Coefficient
The figure compares two pieces of material with different thicknesses and densities but the same area mass. Since both attenuate the same fraction of photons, the mass attenuation coefficient is the same for the two materials. They do not have the same linear attenuation coefficient values.
The relationship between the mass and linear attenuation coefficients is
Mass Attenuation Coefficient (µ/r) = Linear Attenuation Coefficient (µ) / Density (r).
Notice that the symbol for mass attenuation coefficient (µ/r) is derived from the symbols for the linear attenuation coefficient (µ) and the symbol for density (r). We must be careful not to be misled by the relationship stated in this manner. Confusion often arises as to the effect of material density on attenuation coefficient values. Mass attenuation coefficient values are actually normalized with respect to material density, and therefore do not change with changes in density. Material density does have a direct effect on linear attenuation coefficient values.
The total attenuation rate depends on the individual rates associated with photoelectric and Compton interactions. The respective attenuation coefficients are related as follows:
µ(total) = µ(photoelectric) + µ(Compton).
Let us now consider the factors that affect attenuation rates and the competition between photoelectric and Compton interactions. Both types of interactions occur with electrons within the material. The chance that a photon will interact as it travels a 1-unit distance depends on two factors.
One factor is the concentration, or density, of electrons in the material. Increasing the concentration of electrons increases the chance of a photon coming close enough to an electron to interact. In a previous section (Characteristics and Structure of Matter) we observed that electron concentration was determined by the physical density of the material. Therefore, density affects the probability of both photoelectric and Compton interactions.
All electrons are not equally attractive to a photon. What makes an electron more or less attractive is its binding energy. The two general rules are:
1. Photoelectric interactions occur most frequently when the electron binding energy is slightly less than the photon energy.
2. Compton interactions occur most frequently with electrons with relatively low binding energies.
In the previous section referred to above we observed that the electrons with binding energies within the energy range of diagnostic x-ray photons were the K-shell electrons of the intermediate- and high-atomic-number materials. Since an atom can have, at the most, two electrons in the K shell, the majority of the electrons are located in the other shells and have relatively low binding energies.
Dependence on Photon Energy
In a given material, the probability of photoelectric interactions occurring is strongly dependent on the energy of the photon and its relationship to the binding energy of the electrons. The figure below shows the relationship between the attenuation coefficient for iodine (Z = 53) and photon energy. This graph shows two significant features of the relationship. One is that the coefficient value, or the probability of photoelectric interactions, decreases rapidly with increased photon energy. It is generally said that the probability of photoelectric interactions is inversely proportional to the cube of the photon energy (1/E3). This general relationship can be used to compare the photoelectric attenuation coefficients at two different photon energies. The significant point is that the probability of photoelectric interactions occurring in a given material drops drastically as the photon energy is increased.
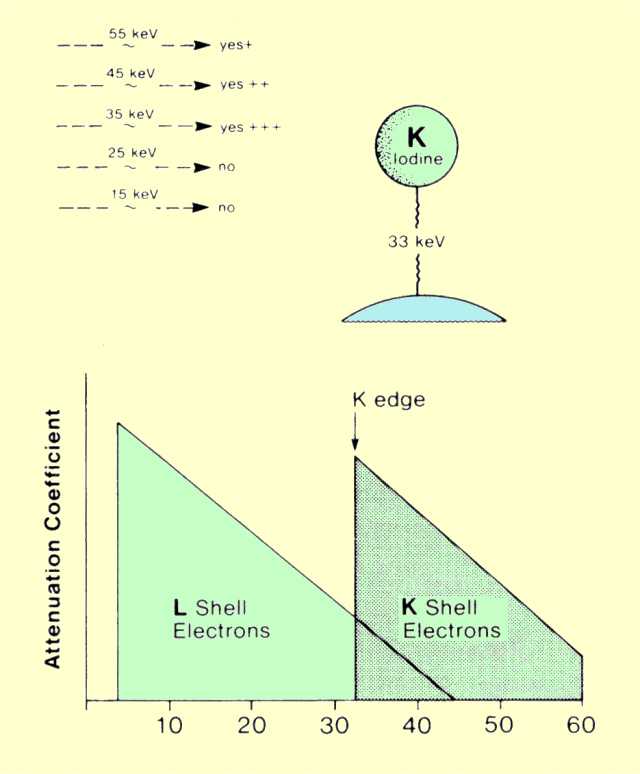
Relationship between the Probability of Photoelectric Interactions and Photon Energy

Material Atomic Number
The probability of photoelectric interactions occurring is also dependent on the atomic number of the material. An explanation for the increase in photoelectric interactions with atomic number is that as atomic number is increased, the binding energies move closer to the photon energy. The general relationship is that the probability of photoelectric interactions (attenuation coefficient value) is proportional to Z3. In general, the conditions that increase the probability of photoelectric interactions are low photon energies and high-atomic-number materials.
Compton Rates
Compton interactions can occur with the very loosely bound electrons. All electrons in low-atomic-number materials and the majority of electrons in high-atomic-number materials are in this category. The characteristic of the material that affects the probability of Compton interactions is the number of available electrons. It was shown earlier that all materials, with the exception of hydrogen, have approximately the same number of electrons per gram of material. Since the concentration of electrons in a given volume is proportional to the density of the materials, the probability of Compton interactions is proportional only to the physical density and not to the atomic number, as in the case of photoelectric interactions. The major exception is in materials with a significant proportion of hydrogen. In these materials with more electrons per gram, the probability of Compton interactions is enhanced.
Although the chances of Compton interactions decrease slightly with photon energy, the change is not so rapid as for photoelectric interactions, which are inversely related to the cube of the photon energy.
Direction of Scatter
It is possible for photons to scatter in any direction. The direction in which an individual photon will scatter is purely a matter of chance. There is no way in which the angle of scatter for a specific photon can be predicted. However, there are certain directions that are more probable and that will occur with a greater frequency than others. The factor that can alter the overall scatter direction pattern is the energy of the original photon. In diagnostic examinations, the most significant scatter will be in the forward direction. This would be an angle of scatter of only a few degrees. However, especially at the lower end of the energy spectrum, there is a significant amount of scatter in the reverse direction, i.e., backscatter. For the diagnostic photon energy range, the number of photons that scatter at right angles to the primary beam is in the range of one-third to one-half of the number that scatter in the forward direction. Increasing primary photon energy causes a general shift of scatter to the forward direction. However, in diagnostic procedures, there is always a significant amount of back- and side-scatter radiation.
Energy of Scattered Radiation
When a photon undergoes a Compton interaction, its energy is divided between the scattered secondary photon and the electron with which it interacts. The electron's kinetic energy is quickly absorbed by the material along its path. In other words, in a Compton interaction, part of the original photon's energy is absorbed and part is converted into scattered radiation.
The manner in which the energy is divided between scattered and absorbed radiation depends on two factors-the angle of scatter and the energy of the original photon. The relationship between the energy of the scattered radiation and the angle of scatter is a little complex and should be considered in two steps. The photon characteristic that is specifically related to a given scatter angle is its change in wavelength. It should be recalled that a photon's wavelength (l) and energy (E) are inversely related as given by:
E = 12.4 / l.
Since photons lose energy in a Compton interaction, the wavelength always increases. The relationship between the change in a photon's wavelength, Dl, and the angle of scatter is given by:
Dl = 0.024 (1 - cos q).
For example, all photons scattered at an angle of 90 degrees, where the cosine has a value of 0, will undergo a wavelength change of 0.024 Å. Photons that scatter back at an angle of 180 degrees where the cosine has a value of -1 will undergo a wavelength change of 0.048 Å. This is the maximum wavelength change that can occur in a scattering interaction.
It is important to recognize the difference between a change in wavelength and a change in energy. Since higher energy photons have shorter wavelengths, a change of say 0.024 Å represents a larger energy change than it would for a lower energy photon. All photons scattered at an angle of 90 degrees will undergo a wavelength change of 0.0243Å The change in energy associated with 90-degree scatter is not the same for all photons and depends on their original energy. The change in energy can be found as follows. For a 110-keV photon, the wavelength is 0.1127 Å. A scatter angle of 90 degrees will always increase the wavelength by 0.0243. Therefore, the wavelength of the scattered photon will be 0.1127 plus 0.0243 or 0.1370. The energy of a photon with this wavelength is 91 keV. The 110 keV photons will lose 19 keV or 17% of their energy in the scattering process. Lower energy photons lose a smaller percentage of their energy.
COMPETITIVE INTERACTIONS
As photons pass through matter, they can engage in either photoelectric or Compton interactions with the material electrons. The photoelectric interaction captures all photon energy and deposits it within the material, whereas the Compton interaction removes only a portion of the energy, and the remainder continues as scattered radiation. The combination of the two types of interactions produces the overall attenuation of the x-ray beam. We now consider the factors that determine which of the two interactions is most likely to occur in a given situation.
The energy at which interactions change from predominantly photoelectric to Compton is a function of the atomic number of the material. The figure below shows this crossover energy for several different materials. At the lower photon energies, photoelectric interactions are much more predominant than Compton. Over most of the energy range, the probability of both decreases with increased energy. However, the decrease in photoelectric interactions is much greater. This is because the photoelectric rate changes in proportion to 1/E3, whereas Compton interactions are much less energy dependent. In soft tissue, the two lines cross at an energy of about 30 keV. At this energy, both photoelectric and Compton interactions occur in equal numbers. Below this energy, photoelectric interactions predominate. Above 30 keV, Compton interactions become the significant process of x-ray attenuation. As photon energy increases, two changes occur: The probability of both types of interactions decreases, but the decrease for Compton is less, and it becomes the predominant type of interaction
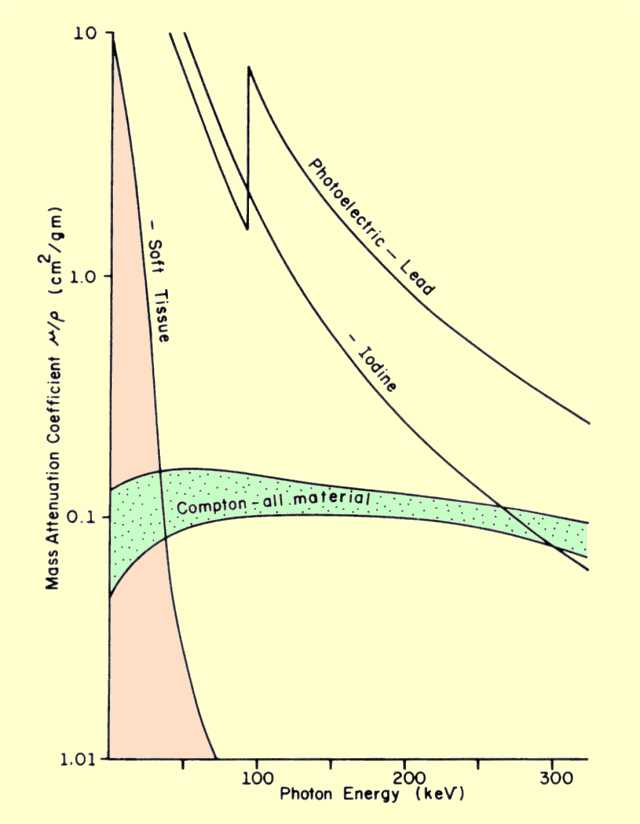
Comparison of Photoelectric and Compton Interaction Rates for Different Materials and Photon Energies
In higher-atomic-number materials, photoelectric interactions are more probable, in general, and they predominate up to higher photon energy levels. The conditions that cause photoelectric interactions to predominate over Compton are the same conditions that enhance photoelectric interactions, that is, low photon energies and materials with high atomic numbers.
The total attenuation coefficient value for materials involved in x-ray and gamma interactions can vary tremendously if photoelectric interactions are involved. A minimum value of approximately 0.15 cm2/g is established by Compton interactions. Photoelectric interactions can cause the total attenuation to increase to very high values. For example, at 30 keV, lead (Z = 82) has a mass attenuation coefficient of 30 cm2/g.
Attenuation
As a photon makes its way through matter, there is no way to predict precisely either how far it will travel before engaging in an interaction or the type of interaction it will engage in. In clinical applications we are generally not concerned with the fate of an individual photon but rather with the collective interaction of the large number of photons. In most instances we are interested in the overall rate at which photons interact as they make their way through a specific material.
Let us observe what happens when a group of photons encounters a slice of material that is 1 unit thick, as illustrated in the figure below. Some of the photons interact with the material, and some pass on through. The interactions, either photoelectric or Compton, remove some of the photons from the beam in a process known as attenuation. Under specific conditions, a certain percentage of the photons will interact, or be attenuated, in a 1-unit thickness of material.

Linear Attenuation Coefficient
The linear attenuation coefficient (µ) is the actual fraction of photons interacting per 1-unit thickness of material. In our example the fraction that interacts in the 1-cm thickness is 0.1, or 10%, and the value of the linear attenuation coefficient is 0.1 per cm.
Linear attenuation coefficient values indicate the rate at which photons interact as they move through material and are inversely related to the average distance photons travel before interacting. The rate at which photons interact (attenuation coefficient value) is determined by the energy of the individual photons and the atomic number and density of the material.
Mass Attenuation Coefficient
In some situations it is more desirable to express the attenuation rate in terms of the mass of the material encountered by the photons rather than in terms of distance. The quantity that affects attenuation rate is not the total mass of an object but rather the area mass. Area mass is the amount of material behind a 1-unit surface area, as shown below. The area mass is the product of material thickness and density:
Area Mass (g/cm2) = Thickness (cm) x Density (g/cm3).
The mass attenuation coefficient is the rate of photon interactions per 1-unit (g/cm2) area mass.

Mass Attenuation Coefficient
The figure compares two pieces of material with different thicknesses and densities but the same area mass. Since both attenuate the same fraction of photons, the mass attenuation coefficient is the same for the two materials. They do not have the same linear attenuation coefficient values.
The relationship between the mass and linear attenuation coefficients is
Mass Attenuation Coefficient (µ/r) = Linear Attenuation Coefficient (µ) / Density (r).
Notice that the symbol for mass attenuation coefficient (µ/r) is derived from the symbols for the linear attenuation coefficient (µ) and the symbol for density (r). We must be careful not to be misled by the relationship stated in this manner. Confusion often arises as to the effect of material density on attenuation coefficient values. Mass attenuation coefficient values are actually normalized with respect to material density, and therefore do not change with changes in density. Material density does have a direct effect on linear attenuation coefficient values.
The total attenuation rate depends on the individual rates associated with photoelectric and Compton interactions. The respective attenuation coefficients are related as follows:
µ(total) = µ(photoelectric) + µ(Compton).
Let us now consider the factors that affect attenuation rates and the competition between photoelectric and Compton interactions. Both types of interactions occur with electrons within the material. The chance that a photon will interact as it travels a 1-unit distance depends on two factors.
One factor is the concentration, or density, of electrons in the material. Increasing the concentration of electrons increases the chance of a photon coming close enough to an electron to interact. In a previous section (Characteristics and Structure of Matter) we observed that electron concentration was determined by the physical density of the material. Therefore, density affects the probability of both photoelectric and Compton interactions.
All electrons are not equally attractive to a photon. What makes an electron more or less attractive is its binding energy. The two general rules are:
1. Photoelectric interactions occur most frequently when the electron binding energy is slightly less than the photon energy.
2. Compton interactions occur most frequently with electrons with relatively low binding energies.
In the previous section referred to above we observed that the electrons with binding energies within the energy range of diagnostic x-ray photons were the K-shell electrons of the intermediate- and high-atomic-number materials. Since an atom can have, at the most, two electrons in the K shell, the majority of the electrons are located in the other shells and have relatively low binding energies.
Dependence on Photon Energy
In a given material, the probability of photoelectric interactions occurring is strongly dependent on the energy of the photon and its relationship to the binding energy of the electrons. The figure below shows the relationship between the attenuation coefficient for iodine (Z = 53) and photon energy. This graph shows two significant features of the relationship. One is that the coefficient value, or the probability of photoelectric interactions, decreases rapidly with increased photon energy. It is generally said that the probability of photoelectric interactions is inversely proportional to the cube of the photon energy (1/E3). This general relationship can be used to compare the photoelectric attenuation coefficients at two different photon energies. The significant point is that the probability of photoelectric interactions occurring in a given material drops drastically as the photon energy is increased.

Relationship between the Probability of Photoelectric Interactions and Photon Energy
Material Atomic Number
The probability of photoelectric interactions occurring is also dependent on the atomic number of the material. An explanation for the increase in photoelectric interactions with atomic number is that as atomic number is increased, the binding energies move closer to the photon energy. The general relationship is that the probability of photoelectric interactions (attenuation coefficient value) is proportional to Z3. In general, the conditions that increase the probability of photoelectric interactions are low photon energies and high-atomic-number materials.
Compton Rates
Compton interactions can occur with the very loosely bound electrons. All electrons in low-atomic-number materials and the majority of electrons in high-atomic-number materials are in this category. The characteristic of the material that affects the probability of Compton interactions is the number of available electrons. It was shown earlier that all materials, with the exception of hydrogen, have approximately the same number of electrons per gram of material. Since the concentration of electrons in a given volume is proportional to the density of the materials, the probability of Compton interactions is proportional only to the physical density and not to the atomic number, as in the case of photoelectric interactions. The major exception is in materials with a significant proportion of hydrogen. In these materials with more electrons per gram, the probability of Compton interactions is enhanced.
Although the chances of Compton interactions decrease slightly with photon energy, the change is not so rapid as for photoelectric interactions, which are inversely related to the cube of the photon energy.
Direction of Scatter
It is possible for photons to scatter in any direction. The direction in which an individual photon will scatter is purely a matter of chance. There is no way in which the angle of scatter for a specific photon can be predicted. However, there are certain directions that are more probable and that will occur with a greater frequency than others. The factor that can alter the overall scatter direction pattern is the energy of the original photon. In diagnostic examinations, the most significant scatter will be in the forward direction. This would be an angle of scatter of only a few degrees. However, especially at the lower end of the energy spectrum, there is a significant amount of scatter in the reverse direction, i.e., backscatter. For the diagnostic photon energy range, the number of photons that scatter at right angles to the primary beam is in the range of one-third to one-half of the number that scatter in the forward direction. Increasing primary photon energy causes a general shift of scatter to the forward direction. However, in diagnostic procedures, there is always a significant amount of back- and side-scatter radiation.
Energy of Scattered Radiation
When a photon undergoes a Compton interaction, its energy is divided between the scattered secondary photon and the electron with which it interacts. The electron's kinetic energy is quickly absorbed by the material along its path. In other words, in a Compton interaction, part of the original photon's energy is absorbed and part is converted into scattered radiation.
The manner in which the energy is divided between scattered and absorbed radiation depends on two factors-the angle of scatter and the energy of the original photon. The relationship between the energy of the scattered radiation and the angle of scatter is a little complex and should be considered in two steps. The photon characteristic that is specifically related to a given scatter angle is its change in wavelength. It should be recalled that a photon's wavelength (l) and energy (E) are inversely related as given by:
E = 12.4 / l.
Since photons lose energy in a Compton interaction, the wavelength always increases. The relationship between the change in a photon's wavelength, Dl, and the angle of scatter is given by:
Dl = 0.024 (1 - cos q).
For example, all photons scattered at an angle of 90 degrees, where the cosine has a value of 0, will undergo a wavelength change of 0.024 Å. Photons that scatter back at an angle of 180 degrees where the cosine has a value of -1 will undergo a wavelength change of 0.048 Å. This is the maximum wavelength change that can occur in a scattering interaction.
It is important to recognize the difference between a change in wavelength and a change in energy. Since higher energy photons have shorter wavelengths, a change of say 0.024 Å represents a larger energy change than it would for a lower energy photon. All photons scattered at an angle of 90 degrees will undergo a wavelength change of 0.0243Å The change in energy associated with 90-degree scatter is not the same for all photons and depends on their original energy. The change in energy can be found as follows. For a 110-keV photon, the wavelength is 0.1127 Å. A scatter angle of 90 degrees will always increase the wavelength by 0.0243. Therefore, the wavelength of the scattered photon will be 0.1127 plus 0.0243 or 0.1370. The energy of a photon with this wavelength is 91 keV. The 110 keV photons will lose 19 keV or 17% of their energy in the scattering process. Lower energy photons lose a smaller percentage of their energy.
COMPETITIVE INTERACTIONS
As photons pass through matter, they can engage in either photoelectric or Compton interactions with the material electrons. The photoelectric interaction captures all photon energy and deposits it within the material, whereas the Compton interaction removes only a portion of the energy, and the remainder continues as scattered radiation. The combination of the two types of interactions produces the overall attenuation of the x-ray beam. We now consider the factors that determine which of the two interactions is most likely to occur in a given situation.
The energy at which interactions change from predominantly photoelectric to Compton is a function of the atomic number of the material. The figure below shows this crossover energy for several different materials. At the lower photon energies, photoelectric interactions are much more predominant than Compton. Over most of the energy range, the probability of both decreases with increased energy. However, the decrease in photoelectric interactions is much greater. This is because the photoelectric rate changes in proportion to 1/E3, whereas Compton interactions are much less energy dependent. In soft tissue, the two lines cross at an energy of about 30 keV. At this energy, both photoelectric and Compton interactions occur in equal numbers. Below this energy, photoelectric interactions predominate. Above 30 keV, Compton interactions become the significant process of x-ray attenuation. As photon energy increases, two changes occur: The probability of both types of interactions decreases, but the decrease for Compton is less, and it becomes the predominant type of interaction

Comparison of Photoelectric and Compton Interaction Rates for Different Materials and Photon Energies
In higher-atomic-number materials, photoelectric interactions are more probable, in general, and they predominate up to higher photon energy levels. The conditions that cause photoelectric interactions to predominate over Compton are the same conditions that enhance photoelectric interactions, that is, low photon energies and materials with high atomic numbers.
The total attenuation coefficient value for materials involved in x-ray and gamma interactions can vary tremendously if photoelectric interactions are involved. A minimum value of approximately 0.15 cm2/g is established by Compton interactions. Photoelectric interactions can cause the total attenuation to increase to very high values. For example, at 30 keV, lead (Z = 82) has a mass attenuation coefficient of 30 cm2/g.



 من طرف Ø£ØمدØسن الأحد سبتمبر 19, 2010 6:45 am
من طرف Ø£ØمدØسن الأحد سبتمبر 19, 2010 6:45 am